「かたちから自然の摂理を学ぶ」シリーズ3~樹木を流れる水から樹木のデザインを捉える
河川のかたちは水の流れを、道路のかたちは車や人の流れを、ラジエターであれば熱の流れを、生物であれば地球上の物質の流れを、より効率的に流すためのデザイン(かたち)に収斂している。
エイドリアン・ベジャンが唱える「コンストラクタル法則」によれば、樹木は地中の水分を大気に運び、不均衡を均一化するストローのようなものであり、水を運ぶために最も理に適った形状に進化するという。
参考:「かたちから自然の摂理を学ぶ」シリーズ2~樹木が発生するのは水を好むからではない
さて、今回は最適な水の流れをつくりだすための樹木デザインについて見ていきます。
まず、樹木の形を考察する前に樹木を流れる2つの流れを把握します。1つは、前述したように、地中から大気中への水の流れ。そして、もう1つは風によって引き起こされる応力の流れ。これは樹木の存続に関する課題といえます
つまり、樹木は内部を通過する水の流れを良くし、吹きつける風に対する強度を備えた構造となる必要があります。
■樹木の根のデザイン
水の流れを追うために、まず根から始めて、根がこの流れをどう処理すべきかを考えます。
ベジャンは根のあるべき姿をこう説明します。
『流れとかたち』(P.202)より引用開始
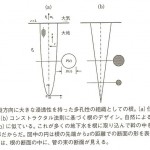
私たちが描き出す木の根は多孔性で、様々な深さで水が系に入れるような(あらゆる側からの)横方向の流れと、地中から水を持ち上げられるような縦方向の流れの、二種類の水の流れを可能にするものでなくてはならない。縦方向の流れ(貫通水路)は横方向の流れよりも抵抗性が低い。
地面に近づくにつれて根の図の幅を拡げ、下方のさまざまなアクセスポイントから入ってきて増える一方の水を処理できるようにしなければならない。
多くの地下水を根に取り込んで幹に引き上げる形は、円形、円錐、先が尖った形、丸い形など様々な形が考えられますが、最も抵抗が少ない根全体の形は円錐形(ニンジン形)であると、ベジャンは予測します。さらに水を吸い上げる1本1本の導管は断面が円形で直径が均一なときに最も抵抗が少なく水が流れやすくなります。円形の断面は、あらゆる方向への曲げに対して大きな抵抗力になるというメリットもあるため、風力に対しても適応的です。
この形はちょうど河川流域の形と似ています。河川流域も縦方向の本流に支流が川岸から横方向に合流するれ根系になっており、水という流動系を一領域から一点に効率的に運ぶには、背後に類似する法則があるということを示唆しています。
■幹と枝のデザイン
次に地上の上部構造をみていきます。
水は上に働き、風に起因する応力は地面へ流れます。幹の中を進む2つの流れのためにふさわし形とはどんな形なのでしょうか。
『流れとかたち』(P.209)
驚くにはあたらないが、私たちが理論に基づいて描き出した幹のデザインは、根のときに得られたものと同じ形になる。今回は下端で太く、高くなるにつれて狭まる。水は途中で低い枝へ分散するので、上に行くほど量が少ないからだ。このデザインは枝にも当てはまる。根や幹と同じで、枝も円錐に近くなるはずだ。
(系は水を吸い上げ、より大きな流路へと吸い込むで)地下に深く潜るほど小さな根が多く見つかるのと同じで、木の上へ行くほど小さな枝が多く見つかる。水を大気中に戻すのには、これが効率的なデザインだからだ。
ベジャンの予測によれば、幹も枝も全て円錐形であることが、水の流れからみても、風力に対応する応力を処理する形としても合理的であると結論づけます。
また、幹の断面積と枝の断面積も明快なルールが存在し、先端に向かって細くなるのに伴う幹の断面積の減少分は、それぞれの幹の区分から生えている横方向の枝の断面積に等しくなると説きます。
イメージ的には、樹木の幹を100本のストローと見立てるとわかりやすいです。最初の枝で10本のストローが分かれ、残りの幹は90本。二番目の枝は9本のストローに別れ、残りの幹は81本となる。これを繰り返しながら、幹と枝のスケールを構成していく、という感じです。
蛇足ですが、レオナルド・ダ・ヴィンチは緻密な観察から上記の法則を既に発見していたといわれていますが、その法則の背後にある構造(水と応力の流れ)までは鮮明にすることができなかったようです。
ちなみに、幹周りの枝や葉や花びらの配列は、螺旋状に配列され、フィボナッチ数列に則って現れるといわれています。
写真は松ぼっくりの模様
この数列もルールを暗記(?)するよりも、木や草が大地から大気中へ水を効率的に移動させるのに適している形であるから、と捉えるのがよいと思います。どの枝(にくっつく葉)も大気中へ水を放出しており、水を蒸散する他の枝から一番遠い所に最も乾いた空気があります。つまり、枝同士の干渉を減らすことが水の蒸散に最も適した形となるのです(注)。
(注)一般的な説明では、枝や葉の配列は、光合成がしやすいように上下の葉の重なりを極力なくす配列であると説明されます。しかし、太陽の光は、毎時真上から来るわけではないので、(光合成がしやすい形態に収斂したという点は間違いではないですが)説明としてはやや疑問が残ります。
もちろん、ベジャンが予想する樹木デザインやフィボナッチ数列は外的要因を限定した時に成立する法則です。現実の樹木は、日射量や気温、風特性、周辺の樹木との相互作用などの複数の物理的要因によって、多様な形態が現れる、というのは外で観察してみて理解するのがよいと思います。
コンストラクタル法則は、多様性が全面に打ち出される生物の背後に潜む主構造を理解するのに役立つ認識である、と捉えるのが良いと思います。
トラックバック
このエントリーのトラックバックURL:
http://www.seibutsushi.net/blog/2014/06/1893.html/trackback