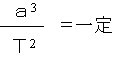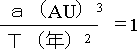ニュートンが定式化した「万有引力」(重力)を、素粒子として扱う立場からは、『重力子』(グラビトン)と呼称します。
素粒子論では、「力が働く時、その力を媒介する素粒子が存在する」という立場に立つので、重力を重力子として扱います。この重力子(グラビトン)の存在はいまだ確認されていないので、素粒子論が仮説として設定したものです。
一方、自然現象としての重力は、古来より物体の落下現象として知られ、16世紀以降の望遠鏡による詳細な天体観測を元にして、ケプラー、ガリレオ、ニュートンの考察により、固定されました。
そこで、重力子(グラビトン)を扱う前に、ニュートンが定式化した古典的な重力をまずは見てみます。

1687年に刊行されたニュートンのプリンシピア(自然哲学の数学的諸原理)。出典:ウイキペディ
1.ケプラー:現実認識への転換、神の秩序=円運動から現実の楕円運動へ
2.ガリレオ:木星の4惑星発見、天体の周回運動の確定
3.ニュートン:重力の定式化=万有引力の設定
本文に行く前にクリックを!!
1.ケプラー:現実認識への転換、神の秩序=円運動から現実の楕円運動へ
幾何学的な美しさから宇宙の構造を考える
ケプラー(1571年~1630年)は、数学の才能に溢れ、大学時代にコペルニクスの地動説を知り、それから惑星の運動について研究を続けました。
1596年に、『宇宙の神秘』という本を出版し、その中で各惑星の天球の大きさ(回転する球の大きさ)と、正六面体(サイコロ形)などの「正多面体」との間には特別な関係があるという説を唱えています。惑星は、正多面体に接する円運動を行っているとするものです。
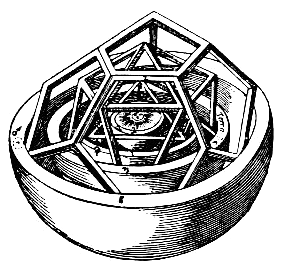
ケプラーの正多面体宇宙モデル。出典:ウイキペディア
宇宙の構造は、円や正多面体という幾何学的な理想形態(神の秩序)の中にあると考えたのです。
神の秩序(円運動)から現実の秩序(楕円運動)への転換
当時、膨大な天体の観測記録を行っていたのがブラーエです。ケプラーはこのブラーエから、「どれだけ美しい宇宙論であっても、実際の天文現象を正しく説明できなければ、それは真理ではない」と教えられ、自らの説を問い直し、ブラーエの残した膨大な観測データをもとに追求した結果、惑星の軌道は美しい円(理想形)ではなく、潰れた楕円であるということを発見しました。
これが、「ケプラーの第一法則」です。そして、太陽系の天体運動を3つの法則にまとめました。
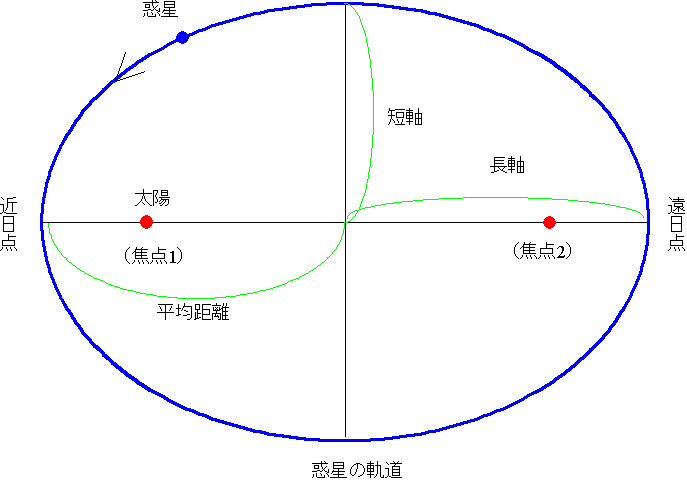
第一法則(だ円軌道の法則)
惑星は太陽を一つの焦点とする楕円軌道上を動く
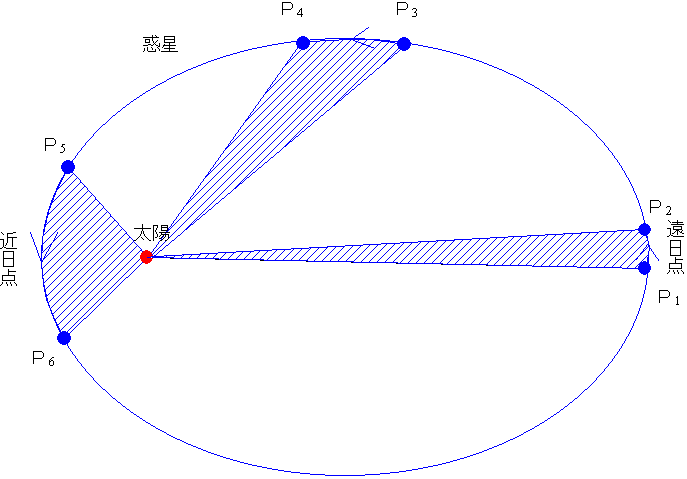
第ニ法則(面積速度一定の法則)
惑星と太陽を結ぶ線分が、一定時間に描く面積は一定である
第三法則(調和の法則)
惑星の公転周期の2乗と惑星の太陽からの距離の3乗の比は、惑星によらず一定である
上記の三法則を視覚的に確認してみます。
第一法則(楕円運動)
第二法則(面積速度一定)
第三法則(調和の法則)
惑星の公転周期をT、惑星と太陽の平均距離をaとすると、Tの2乗とaの三乗との比がどの惑星でも一定になる。
公転周期の単位として年、惑星と太陽の平均距離の単位として天文単位(AU)を使うと、地球の公転周期は1年、地球と太陽の平均距離は1AUなので、この比の値は1ということになる。
金星の公転周期は0.6152年、太陽との平均距離は0.7233AUだから比の値は0.9998、木星の公転周期は11.862年、平均距離は5.2026AUだから比の値は1.0008である。ケプラーの第三法則によって、惑星の間の相互関係を求めることができるようになった。
『山賀進のWeb site』ケプラー [5]から
そして、重力については、以下のように考えました。
「重力とは、類似の物体間の合一しようとする相互的な傾向のことである。それゆえ、石が地球を引き寄せようとする以上に、地球は石を引き寄せる。」「重力が距離に反比例するだけでなく、引き寄せる物体の質量に比例する」とも述べています。
2.ガリレオ:木星の4惑星発見、天体の周回運動の確立
ガリレオ(1564年~1642年)は、当時登場した望遠鏡を自作し、その高性能の望遠鏡により、太陽系を観測し、様々な天体運動を解明していきました。
ガリレオの14倍望遠鏡(分解したもの)

写真出典:現存する ガリレオが製作した2本の望遠鏡 [6]
そして、木星の周りを回っている衛星が、4つあることを発見しました。この発見は、天体の運動モデルとして、一つの天体の周りを、別の天体が回っていることを直接的に観測できた点で画期的です。
左は1610年1月7日の木星(中央)と衛星、右は翌日1月8日の木星と衛星
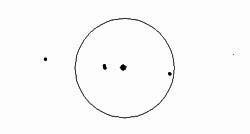
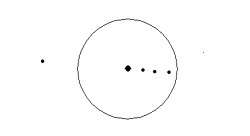
参考:ガリレオ木星衛星発見 [7]
当時提出された地動説(地球が太陽の周りを回っている)や月の衛星説(地球の周りを月が回っている)は、地球と太陽、月と地球の相対的な位置関係の変化を、そのように理論化できるというもので、直接的な観測ではありません。
それに対して、木星と4つの衛星の観測は、衛星の周回運動を直接観測したものです。
4つの衛星は、木星の近傍に必ず存在する。見かけ上、木星の近傍に見えるのではない。
4つの衛星が位置を変えたり、見えなくなったりする現象は、衛星が木星の周りを回っていると仮定すると、観測結果と整合する。
この観測事実を元にして、天体(木星)の周りを別の天体(4つの衛星)が回っているという、天体の周回運動モデルを確立したのです。
ケプラーの楕円運動の定式化は、現象を説明する仮説モデルですが、この周回運動(楕円運動)を天体の実体モデルにしたのが、ガリレオです。そして、衛星の周回運動には、惑星と衛星の間に力が働いているという動力学を想定しました。
3.ニュートン:重力の定式化=万有引力の設定
ケプラーは、重力が地球と石との間で相互的に働いている力であり、距離に反比例し、引き寄せる物体の質量に比例することまで述べています。
その後、ばねの力はその伸びに比例するという「フックの法則」を発見したロバート・フックは、1666年の論文で「惑星の運動は慣性による軌道接線方向への直線運動に中心物体からの引力による中心方向への加速が重ねあわされたものと見ることが出来る」と惑星の楕円軌道が力の合成によるものとしました。
これらの成果を土台に、天体運動を数学的に体系化したのがニュートン(1642年~1727年)です。
ニュートン力学、古典力学の誕生です。
ニュートンは、物体を質点すなわち質量を伴った点として扱い、各質点は力の作用により、運動が変化するとしました。力と運動(速度、加速度)の関係を法則化したのです。
第一法則:外力が加わらなければ、物体は等速直線運動を行う。【慣性の法則】
第ニ法則:物体は加わる力の大きさと方向に加速する。【加速度の法則】
第三法則:二つの物体には相互に同じ大きさの逆向きの力が働く。【作用・反作用の法則】
そして、ケプラーが発見した楕円軌道とフックが考察した力の合成の考え方から、
◆太陽と惑星の間に距離の二乗に反比例する引力が働いている
◆その力は2物体の質量(の積)に比例する
◆その引力は万有=すべての物体間に働いている
とし、『万有引力の法則』として定式化しました。
Fは万有引力の大きさ、M・mは二つの物体質量、rは物体間の距離、Gは万有引力定数
ニュートンの功績は、重力を発見したことではなく、月や惑星に対して働いている力が、地球と地球上の物体の間に働いていると着想した点です。だから、あらゆる物体間に、働く力=万有引力を設定し、その数学的な定式化を行ったのです。地球上の物体が、落下する力は地球の引力(重力)に基づき、その落下速度は数学的に計算できることを明らかにしたのです。
ニュートンの立場は、観測事実、現象事実があり、その事実関係の中に法則(数学的整合性)を見出し、その数学的計算で、物事が予測できれば十分であるという立場を徹底させました。
『ニュートンは重力の原因や成因の追及を放棄し、力の数学的法則の確立を提起した。』
『ニュートンの公式的立場は、「万有引力の本質は何か」とか「何故万有引力が存在するのか」といった存在論上の問題は自然哲学の問うところではないし、あるいは「万有引力は空間をどのように伝播するのか」とか「万有引力は何を介して対象物体に届くのか」といった事柄に頭を悩ますには及ばない。といったものである。』
『宇宙空間に充満している微細物質の渦動が天体に作用する、といったような機械論はニュートンが退けてしまった。』
「重吾@中井沢の本棚」『磁力と重力の発見〈3〉近代の始まり』(山本 義隆) [8]
私たちが小学校から学ぶ力学のほとんどはニュートン力学であり、実用という点では、大砲の弾道計算、ロケットの地球脱出速度の計算、静止軌道上を回る人工衛星の周回速度の計算など、マクロな物体運動では、十分に現実の役に立っています。
最後に太陽系の惑星の公転運動と楕円軌道の形成について、簡単にふれておきます。
太陽系は、最初は小さなチリ(星雲)が回転していた。そのチリが集まって、中心に太陽ができ、周辺に小惑星ができます。そして、チリが一層合体して、現在の惑星が出来上がったのです。もともとが、回転していたチリが集合してものが惑星ですので、最初からもっていた回転運動が保存され、太陽を回る公転運動となったのです。
また、回転運動では、円運動と楕円運動は数学的には同じものです。円運動は、楕円運動の特殊状態です。特殊な条件で初めて円運動が持続します。惑星生成の過程では、惑星により小さな小惑星が合体するので、複雑な力が働き、円運動の特殊条件が壊れ、楕円運動となって安定化したと考えられています。
参考:太陽系の形成と進化 [9]
それでは、19世紀末から20世紀初頭に入り、なぜ、ニュートンの古典力学に対する疑問が登場したのでしょうか。
ニュートンの古典力学では説明できない天体運動の現象がその後見つかったのでしょうか。
或いは、数学的考察から、ニュートンの古典力学の変更を必要としたのでしょうか。
次回は、ニュートン力学を塗り重ねたアインシタインを扱ってみます。